image de Serge Cecconi (IMAG)
Nous allons dans ce module conjecturer un lien entre le sens de variation d’une fonction et les propriétés de sa dérivée.
Reprendre les quatre
fonctions de la onzième
séance
| Problème 1 Appelons
x le prix de la
place et n l’écart de ce prix par rapport à 3
F : Appelons f(n) la recette.
|
Problème 2 Appelons m1 la longueur du premier morceau, m2 la longueur du 2ème morceau et l la longueur totale. La somme des aires du cercle et du carré est :
|
| Problème 3 Appelons y le côté de la feuille carrée de métal blanc et x le côté du petit carré que l’on découpe. Le volume de la boîte est alors :
|
Problème 4 Appelons r le rayon de la boîte cylindrique et h sa hauteur. La surface de métal utilisée est alors :
|
Pour chacune de ces fonctions, construire les graphes
de la fonction et de sa dérivée dans une même fenêtre.
Observez les quatre fenêtres graphiques obtenues.
Que semble-t-il se passer pour la dérivée lorsque la fonction
passe par un extremum ? Vérifier votre conjecture par le
calcul.
Conjecturer des liens entre le sens de variation de la fonction
et les propriétés de sa dérivée.
Le
mode d'emploi TI
| Problème 1 Définition
de la recette de cinéma |
 |
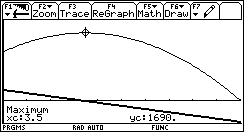| Problème 2 Définition
de la somme des aires |
 |
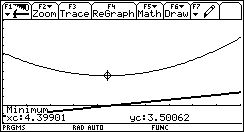| Problème 3 Définition
du volume de la boîte |
 |
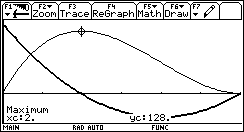| Problème 4 Définition
de la surface de métal utilisée |
 |
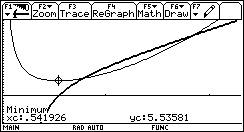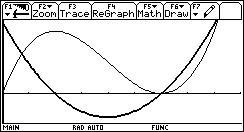
Reprendre la fonction du problème 3 et tracer les courbes représentant la fonction et sa dérivée sur un intervalle plus grand (bien que l’intervalle n’ait alors aucun sens physique). Dresser alors le tableau de variation de la fonction, ainsi que celui de sa dérivée.
Applications
Pour les fonctions suivantes, calculer la dérivée puis étudier le signe de la dérivée. Faire ensuite le tableau de variation de la fonction, en y indiquant le signe de la dérivée :
HOME
(touche STO)
(d
s’obtient à l’aide de 2nd 8)
(choix
arbitraire d’une ficelle de 10 cm de long)
(choix
arbitraire d’une boîte de 12 cm de côté)
