La TI-92 en Première S

Nous allons dans ce module conjecturer avec CABRI puis résoudre un problème pris dans le livre de géométrie de Terracher : n^o 93 page 129 (Hachette, édition de 1991)

Etant donnés deux réels positifs x et y, on désigne par moyennes arithmétique, géométrique et harmonique les nombres respectivement désignés par a, g et h et définis par :

1° Construction des moyennes
On considère trois points A, I, B alignés dans cet ordre avec AI = x et IB = y et l'on désigne par O le milieu de [AB].
On effectue alors les constructions suivantes :

un demi-cercle C de diamètre [AB] ;
la perpendiculaire à (AB) issue de I qui coupe C en M ;
le point H projeté orthogonal de I sur [OM]

a) Faire une figure illustrant ces données.
b) A l'aide des relations métriques dans le triangle rectangle, calculer MO, MI et MH en fonction de x et de y.

2° Comparaison des moyennes
Sans calcul, comparer a, g et h et examiner à l'aide de la figure les cas d'égalités.

Lecture de la construction	Construction Cabri
Lancer Cabri Créer les trois points A, I, B alignés dans cet ordre. Les nommer au fur et à mesure. O est milieu de [AB]	APPS 8 *Geometry* 3 *New* Variable : *Moyennes* F2 *Line* - F2 *Point on Object* F4 3 *Midpoint*
Construire - le cercle C de centre O passant par B - un demi-cercle sur C, - le segment [AB] effacer le cercle et la droite support de A, I, B· la perpendiculaire à (AB) issue de I qui coupe C en M ; le point H projeté orthogonal de I sur [OM] : construire d'abord le segment [OM], puis la perpendiculaire à [OM] passant par I ; créer alors le point H	F3 1 *Circle* F3 2 *Arc* - F2 5 *Segment* F7 1 HIDE SHOW F4 1 *Perpendicular Line* F2 3 *Intersection Point* F2 5 *Segment* F4 1 *Perpendicular Line* F2 3 *Intersection Point*	Figure finale :

Les grandeurs représentant les moyennes sont sur la figure :
Vérifier par le calcul que MO = a.
Puis montrer que MI = g et MH = h.

Retour à la construction : déplacer la figure vers la droite de l'écran (en maintenant la touche 2nd appuyée, on peut déplacer la figure globalement à l'aide de la souris).

A l'aide la macro « Compas » (F4 8 Compass), reporter les longueurs x, y, a, g, h afin qu'elles aient toutes une origine placée sur une même verticale, à gauche de l'écran.

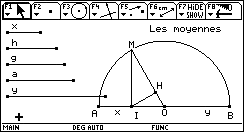
Déplacer le point I sur le segment [AO]. Que conjecturez-vous ?
Examiner à l'aide de la figure les cas d'égalités.

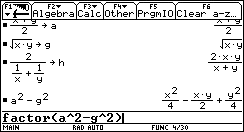
On pourra d'abord effectuer les calculs « à la main », puis prendre la TI-92 :

La TI-92 en Première S

Comparaison de moyennes avec Cabri