La TI-92 en Première S

Aire d’un triangle équilatéral avec CABRI

***

image de Serge Cecconi (IMAG)

Nous allons dans ce module visualiser avec CABRI la variation de l’aire d’un triangle équilatéral mobile inclus dans un triangle équilatéral fixe.
L’idée est partie d’un exercice du livre de géométrie de Terracher : no 70 page 126 (Hachette, édition de 1991)

Enoncé du problème

Soit ABC un triangle équilatéral de côté a.
Etant donné un réel x non nul, on définit les points P, Q, R par :
, , .

1o/ Cas particuliers : faire une figure illustrant ces données pour

On revient au cas général pour la suite du problème et on choisit x dans l’intervalle [0, 1]. (Traduire géométriquement ce que cela signifie).

2o/ Exprimer en fonction de x et de a.
En déduire en fonction de x et de a.
Indication :  et .

3o/ Comparer les triangles APR, BQP et CRQ. En déduire que le triangle PQR est équilatéral.

4o/ Montrer que le triangle PQR a même centre de gravité que le triangle ABC.

5o/ Pour quelle(s) valeur(s) de x le triangle PQR a-t-il ses côtés orthogonaux à ceux du triangle ABC (c’est à dire : ) ?

 

Construction CABRI (on se limitera à x variant dans l’intervalle [0, 1])

Lecture de la construction

Construction Cabri

 
Lancer Cabri

Créer les points B et C sur une droite horizontale, en bas de l’écran
Les nommer au fur et à mesure.
Construire A, sommet du triangle équilatéral

Construire les segments [AB], [BC], [CA].

 APPS 8 Geometry
3 New
Variable : Airemini

F2 4 Line - F2 2 Point on Object
F3 1 Circle
F2 3 Intersection Point
F2 5 Segment

  
Créer le point P, objet sur [AB].
Construire alors :
Q sur [BC]
R sur [CA]
Construire le segment [PR] et le triangle PQR
Mesurer alors :
- la longueur AP (c’est x.AB)
- la longueur PR
- l’aire de PQR
Placer vos mesures en haut à droite de l’écran.
F2 2 Point on Object

F4 8 Compass

F2 5 Segment
F3 3 Triangle
F6 1 Distance & Length
F6 2 Area

 Figure finale :

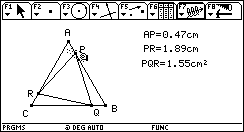
Manipulations de la figure : Placer P au tiers puis au milieu du segment [AB]. Observez la figure. Comparer les données aux mesures du triangle ABC dans chaque cas.
Facultatif : Vérifier que les triangles ABC et PQR ont même centre de gravité.

Collecter les données

Avant de collecter les données, effectuer dans HOME :
Delvar sysdata

F6 7 Collect Data puis effectuer dans l’ordre :
2 Define Entry : montrer les nombres AP, PR et PQR
F6 7 Collect Data 1 Store Data
F7 3 Animation : tirer sur le point P (le ressort doit apparaître) à l’aide de la touche Lock (maintenue appuyée) et de votre souris. Laisser le temps aux données d’être collectées (P doit décrire tout le segment [AB])
Vérifier alors que les données sont bien dans la machine : APPS 6 Data/Matrix Editor 1 Current

Représentation graphique des données collectées

a) Tracé de PR en fonction de AP

Toujours dans le Data/Matrix Editor :
F2 Plot Setup
F1 Define : Plot Type........ 2 xyline
x.........c1
y.........c2
Enter
GRAPH

Lire les coordonnées du minimum, comparer aux données de départ.

b) Tracé de l’aire de PQR en fonction de AP

Toujours dans le Data/Matrix Editor :
F2 Plot Setup
F1 Define : Plot Type........ 2 xyline
x.........c1
y.........c3
Enter
 GRAPH

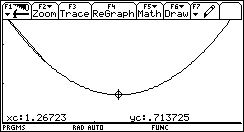Lire les coordonnées du minimum, comparer aux données de départ.

PARTAGE D’ECRAN

MODE Split Screen
3 LEFT-RIGHT
Split 1 App........8 Geometry
Split 2 App........4 Graph

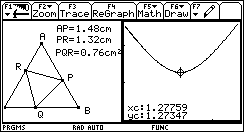Pour naviguer d’une fenêtre à l’autre, appuyer sur la touche 2nd APPS.

Etude algébrique du côté et de l’aire du triangle PQR

Définir dans HOME les fonctions f et g définies par :

et .

Montrer que le côté PR du triangle PQR est proportionnel à f(x).
Montrer que l’aire du triangle PQR est proportionnelle à g(x).
Tracer alors les représentations graphiques de ces deux fonctions

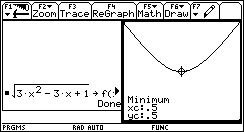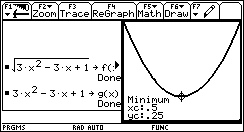En déduire les valeurs exactes du minimum de PR et de l’aire.
Remarque : En effectuant un changement d’unités, on pourra vérifier que PQ et , définie dans HOME, ont bien les mêmes graphes.

***Télécharger la fiche

***

***