image de Serge Cecconi (IMAG)
Cette séance fut la première initiation au module CABRI de la TI-92. Elle fut très fastidieuse car les élèves ont eu beaucoup de mal à se familiariser avec l'interface du module de géométrie. Nous avons donc avancé à tous petits pas et une séance supplémentaire a été consacrée à la réalisation de la macro-construction proposée ci-dessous.
Principe
de base de la construction
Le problème que l'on se pose :
A et B étant deux points du plan, on cherche s'il
existe un point M vérifiant 
(1).
, avec 
équivaut à 
.
Il existe donc un unique point M vérifiant (1)
lorsque .
Ce point est appelé barycentre des points A(a), B(b).
~~~~~~~
 |
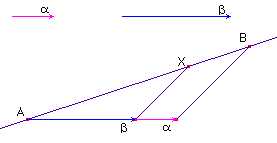Sur la figure ci-contre, écrire
le théorème de Thalès et montrer que :
Qui est donc ce point X ? |
Construction
du barycentre M de A(a),
B(b)
Lancer CABRI
|
APPS 8 Geometry
3 New Variable
: bar2pts
|
Observations de la figure
. Qualitatif
Où est le point M si a = 0, b = 0, a = b ?
En bougeant a et/ou b, placer M à gauche de A.
Si
est petit,
de sens opposé de plus en plus grand, que fait le point M ? Pourquoi ?
. Quantitatif
Mesurer les segments a et b.
- pour a = 1 et b = 2, vérifier les résultats du cours,
- pour a = -1 et b = 3 également.
Dégager des règles de la position du barycentre M sur la droite (AB). Justifier.
La
macro-construction Bar2pts
|
|
Test
de la macro : construction du barycentre de 3 points A(a), B(b), C(g)
|
|
Pas
de document Word correspondant...
