image de Serge Cecconi (IMAG)
Nous allons dans ce module :
1. observer les propriétés fondamentales des transformations du programme de première S : translation, réflexion, rotation et homothétie en transformant une même figure de base.
2. construire l’image de cette même figure de base par des transformations qui transforment vraiment. On pourra ainsi remarquer que les propriétés fondamentales de conservation observées au 1. ne sont pas toujours vérifiées.
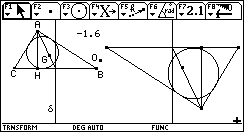
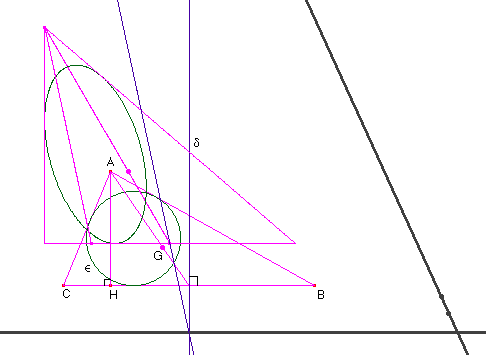
![]() Reproduire dans le
module CABRI de votre TI-92 la figure de base :
Reproduire dans le
module CABRI de votre TI-92 la figure de base :
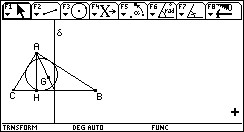
Remarque : il vaudrait mieux que cette figure soit prête dès le début de la séance, car les élèves les moins doués prennent à peu près toute l'heure pour la réaliser, ce qui n'est pas le but recherché ! Ainsi, dès le début de la séance, il vous suffira de copier sur les machines de vos élèves la figure de base (à l'aide du câble de transfert).
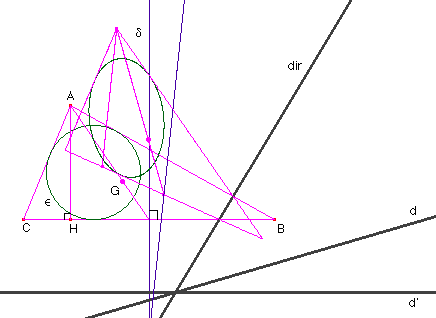
![]() Images de la figure
de base par les transformations du programme de première
S :
Images de la figure
de base par les transformations du programme de première
S :
translation, réflexion, rotation et homothétie.
T |
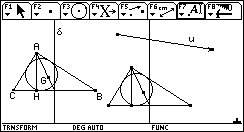 |
R |
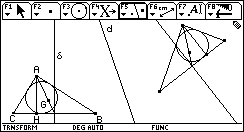 |
R |
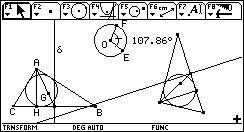 |
H |
 |
Réalisation des figures
Les transformations se trouvent dans le menu F5 :
| 1 :
Translation 2 : Rotation 3 : Dilatation 4 : Reflexion 5 : Symmetry 6 : Inverse |
homothétie réflexion ou symétrie axiale symétrie centrale (rotation d’angle inversion (n’est pas au programme du lycée) |
Commentaires sur l’utilisation de ces commandes :
- La commande F5 2 rotation demande que l’on ait défini un angle par sa valeur numérique. C’est pourquoi on a défini un angle
que l’on mesure à l’aide de la commande F6 3 Angle. L’avantage de placer E et F sur un cercle de centre O est que l’on peut agir sur cet angle simplement en déplaçant E ou F. Le centre de la rotation est le point O.
- La commande F5 3 dilatation demande la valeur numérique du rapport d’homothétie. On définit donc ce nombre à l’aide de F7 6 Numerical Edit. Le centre est le point O.
Observation des figures
Pour chaque transformation, quelles sont les propriétés de la figure initiale que l’on retrouve sur la figure finale ? (parallélisme ? orthogonalité ? distance ? barycentre ? contact ?).
Pour chacune de ces transformations, on peut animer les éléments de base. Par exemple, pour l’homothétie, animer le rapport (F7 3 Animation) et pour la rotation, animer l’angle.
![]() Images de la figure
de base par des transformations qui transforment vraiment...(just
for fun !)
Images de la figure
de base par des transformations qui transforment vraiment...(just
for fun !)
transformation de la figure de base par une inversion f1
On utilise la commande F5 6 Inverse.
Cette transformation se fait par rapport à
un cercle que l’on ajoutera à la figure.
Pour obtenir l’image du
cercle inscrit par cette transformation, on demandera
l’image d’un point sur ce cercle puis on demandera le
lieu décrit par l’image obtenue (F4 A Locus).
Procéder de même pour les autres éléments.
transformation de la figure de base par " symétrie par rapport à un cercle " f2
| On se donne un
cercle W . Imaginons une application du plan dans lui-même qui associe à un point M quelconque un point M1 tel que : si la demi-droite [OM) coupe W en N, alors N est milieu de [MM1]. Faire la figure. |
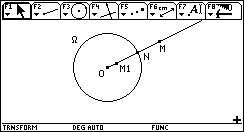 |
Commençons par réaliser une macro-construction " symétrie cercle " :
| Pour la
réalisation de la macro, on suivra les étapes
suivantes : F4
6 Macro Construction |
 Nom de la macro : symcrcle (à rentrer dans la boîte de dialogue Variable) |
On applique ensuite cette macro-construction aux éléments de la figure de base.
Pour obtenir l’image du cercle inscrit par cette transformation, on demandera l’image d’un point sur ce cercle (F4 6 Macro Construction 1 Execute Macro) puis on demandera le lieu décrit par l’image obtenue (F4 A Locus). Procéder de même pour les autres éléments.
| On obtient la jolie figure suivante : |
|
transformation de la figure de base par d’autres transformations (f3, f4 et f5)
|
transformation par f3 |
|
transformation par f4 |
|
transformation par f5 |
![]() Le point sur la
conservation
Le point sur la
conservation
Remplir le tableau suivant en mettant des croix lorsque vous pensez que la propriété est conservée.
transformations |
du |
programme |
de PS |
just |
for |
fun |
|||
|
translation |
rotation |
homothétie |
réflexion |
f1 |
f2 |
f3 |
f4 |
f5 |
alignement |
|||||||||
parallélisme |
|||||||||
orthogonalité |
|||||||||
distance |
|||||||||
angles orientés |
|||||||||
barycentre |
|||||||||
contact |
|||||||||
cocyclicité |
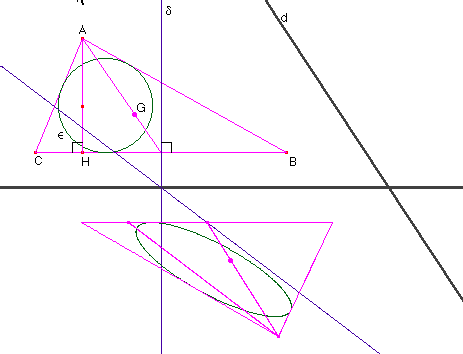
![]() Quelques figures
CABRI, pour le plaisir des yeux
Quelques figures
CABRI, pour le plaisir des yeux
"Symétrie par rapport à un cercle" f2
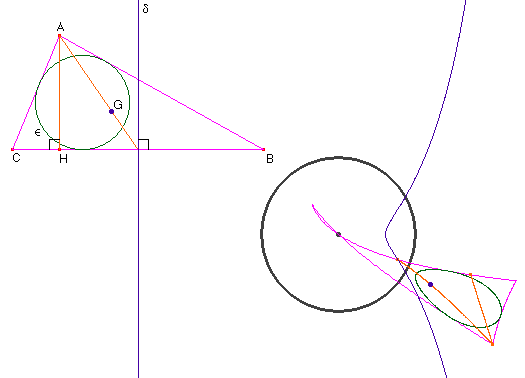
image par inversion f1
