image de Serge Cecconi (IMAG)
Ce module est une séance de correction d’exercices. Il doit vous permettre d’utiliser votre TI-92 comme aide à la résolution d’exercices de trigonométrie. Il devrait vous aider à décider par la suite, si oui ou non il faut prendre votre TI pour traiter un problème de trigo.
Les exercices sont tous tirés du manuel de Terracher (géométrie 1991). Les énoncés sont rappelés.
Exercice no40 page
153 : Vrai ou Faux ?
ne dépend pas de x.
~~~~~•~~~~~
A la TI-92, calculer cette expression.
Expliquer le résultat donné par la calculatrice. (On pourra
grouper les termes convenablement deux à deux).
Exercice no42 page
153
Calculer 
.
~~~~~•~~~~~
Remplir donc avec votre TI :
 |
 |
Preuve par le calcul : A l’aide de la
relation 
, calculer 
.
En déduire la valeur exacte de 
.
Calculer alors 
.
Exercice no43 page
153
Calculer :
~~~~~•~~~~~
Comment gagner du temps avec sa TI ?
On reconnaît une valeur commune dans ces deux expressions :
.
Nous allons donc stocker au préalable dans
la variable t : 
t
puis on calcule alors :
.
Que donne la TI ? Justifier.
Exercice no44 page
153
Après avoir vérifié que 
et que 
,
montrer que :
.
~~~~~•~~~~~
Pour la vérification préliminaire, on contrôle
simplement, avec la TI, la valeur de 
puis celle de 
.
Que donne la TI pour le résultat à démontrer, directement ? Avec la commande tCollect ? Avec la commande tExpand ?
Exercice no45 page
153
Soit x un
réel différent de 
.
Montrer que : 
Application : Calculer 
.
~~~~~•~~~~~
La TI vous aide-t-elle à montrer directement l’égalité demandée ?
Et en mettant l’égalité sous la forme : 
?
Par le calcul, développer 
...
Avec la TI, calculer 
pour 
.
(On stockera d’abord 
dans
x : 
)
Comparer avec ce que vous donne la TI pour 
.
Recommencer pour 
.
Equations trigonométriques
Exercice no53 page
153
Résoudre l’équation suivante et représenter
les solutions sur le cercle trigonométrique :
.
Indication :
effectuer un changement de variable.
~~~~~•~~~~~
Apprendre à traduire certains résultats donnés par la TI ...
A la TI : solve(,x)
fournit la réponse un tant soit peu barbare suivante :
Les nombres @n1, @n2, @n3 etc... représentent des
entiers quelconques.
Traduire, en clair, ce que la machine vous a renvoyé.
Justifier ces résultats. (On pourra utiliser l’indication
puis résoudre à la TI les deux équations 
).
Représenter les solutions sur le cercle trigonométrique.
Exercice no52 page
153
Résoudre les équations suivantes et représenter les solutions sur le cercle trigonométrique :
~~~~~•~~~~~
Résoudre avec la TI l’équation du a). Traduire
en clair ce qu’elle répond.
Justifier par le calcul (on factorise...). On pourra résoudre à
la TI les deux équations 
.
Résoudre avec la TI l’équation du b). Les résultats donnés par la machine sont-ils exploitables ?
Après avoir transformé l’équation b) en une égalité de cosinus, la résoudre puis représenter les solutions sur le cercle trigonométrique.
Exercice no56 page
153
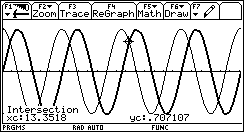
Quel est le nombre de points d’intersection des courbes représentatives de f et de g ?
 |
~~~~~•~~~~~
C’est le nombre de solutions de l’équation 
dans
l’intervalle 
.
Résoudre cette équation avec la TI. En déduire le nombre de
solutions comprises dans cet intervalle.
Exercice no57 page
153 : un problème d’extremums
1o Montrer que pour tout réel x :
 2o En déduire :
|
|
~~~~~•~~~~~
A la TI : tExpand(
).
En déduire le 1o.
On pourra résoudre à l’aide de la TI les équations 
pour
trouver les extremums demandés.
Vérifier avec la TI à l’aide des fonctions fMin et fMax.
Résoudre à la TI la dernière équation.
Moralité du module
Pour traiter un exercice de trigonométrie avec votre TI-92, il faut :
- Essayer le calcul direct
- Essayer la commande tExpand
- Essayer la commande tCollect
Bien souvent, les actions des deux commandes précédentes sont complémentaires et vous seront utiles dans votre phase de vérification des résultats si le calcul direct n’a pas abouti.
Pour résoudre une équation trigonométrique avec la
TI, il sera souvent préférable de la mettre sous la forme 
. Si
l’équation de départ comportait le rapport de deux
expressions de x, il
vaut mieux réduire au même dénominateur et montrer que le
numérateur est nul.
;
.
