image de Serge Cecconi (IMAG)
Nous allons dans ce module construire une fonction
polynôme définie par : 
,
ainsi que les composées de ce polynôme avec les fonctions de
référence : 
.
Définition du polynôme
|
|
Définition des fonctions
composées
|
|
En jouant sur la taille de la fenêtre graphique (xmin,
xmax, ymin, ymax) dans WINDOW , essayez de construire les
composées telles qu'elles sont représentées ci-dessous.
Associez alors chaque graphique et sa composée.
Inscrire sur chaque graphique la fonction composée, sous deux
formes : la forme composée avec f (exemple
: 
) et l'expression analytique
complète, obtenue dans le menu HOME (pour l'exemple, ce sera : 
) puis dresser le tableau de variation de la fonction composée
(vérifier qu'il est bien compatible avec le théorème sur le
sens de variation des fonctions composées).
|
|
|
|
|
|
|
|
|
|
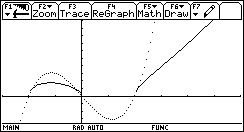
Superposition de courbes :
Il est souvent plus aisé de comprendre le sens de variation de la fonction composée lorsque l'on superpose les deux courbes : la représentation graphique de f et celle de sa composée.
Ainsi, sur ce schéma, essayer d'expliquer de quelle composée il s'agit.
Chaque courbe possède un attribut de tracé graphique.
Par défaut, cet attribut est le trait plein (F6 Styles
dans Y=).
Voici une autre composée, la reconnaissez-vous ?
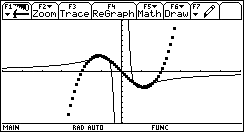
Lorsque vous superposez des courbes, il serait judicieux de laisser le curseur visible lorsque la courbe se dessine (F1 9 leading cursor ON).
HOME
(touche STO)
