Le labyrinthe
Sophie veut aller de D à A par différents chemins. A chaque carrefour, elle gagnera autant de centaines de francs que la plus grande racine de l'équation , où x représente l'inconnue.
Attention aux racines négatives qui font perdre de l'argent et aux trinômes sans racines qui bloquent le passage ! Combien dénombrez-vous de chemins possibles ? Expliciter ces chemins, calculer les sommes obtenues par Sophie pour chaque chemin et conclure en répondant à la question suivante :
Quel chemin doit-elle emprunter pour s'offrir la plus belle maquette de château possible ?
Barycentre
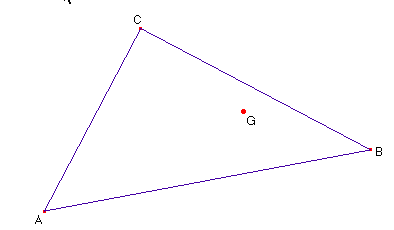
C appartient au cercle E de diamètre [AB]. G est barycentre de A1B4C3.
Faire la construction sur la TI-92.
Quel est le lieu de G lorsque C décrit E ? Dessiner ce lieu sur la figure suivante et énoncer votre conjecture.
Programmation
On cherche deux nombres a et b dont on connaît la somme S et le produit P.
On rappelle que a et b sont les racines de l'équation :
Ecrire un programme avec S et P comme entrées, a et b comme sorties, avec discussion sur l'existence des racines.
Vous donnerez le listing de votre programme sur la copie.
Application : utilisez votre programme pour résoudre l'équation ci-dessus avec :
1) S = 1, P = 3
2) S = 1, P = -2
3) S =
, P = -2
Contrôlez les résultats de votre programme dans le menu « Home » de la calculatrice :
1) dans les trois situations ci-dessus
2) lorsque S et P sont quelconques.
Système
Résoudre, en fonction de a, le système suivant d'inconnues x, y et z :
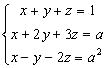
Pour quelle(s) valeur(s) de a obtient-on y = 0 ?
Pour quelle(s) valeur(s) de a obtient-on z = 0 ?
Peut-on avoir à la fois y = 0 et z = 0 ?
Télécharger
la fiche
