Résolution graphique d’équations du second degré
L’Orthogone de Lill sur CABRI
image de Serge Cecconi (IMAG)
L'orthogone de Lill fournit une
construction géométrique des solutions d'une équation du
second degré.
Ce problème a été proposé
par l’IREM de Strasbourg.
Les élèves ont eu cet
exercice à traiter en devoir maison avant de faire la fiche TI
qui suit.
L'Orthogone
de Lill : le problème
On se propose de
résoudre graphiquement toute équation du second degré,
soit :  Dans un repère orthonormé  ,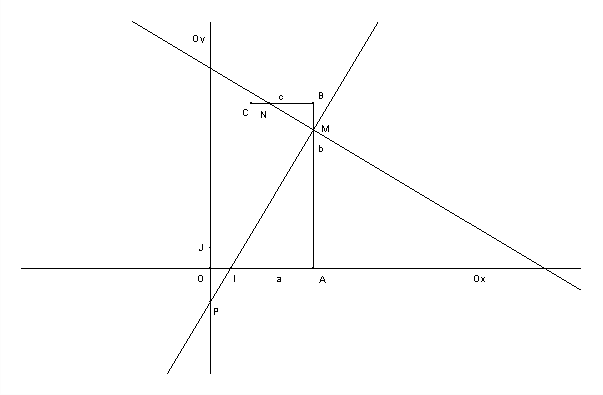
on place les points I, A, B et C définis par :
et   A tout point P de coordonnées (0, a ) on associe le point N de la droite (BC) par la construction indiquée.
|
La
construction de l'Orthogone de Lill : synthèse
Le cercle C de diamètre [IC] coupe la droite (AB) en au plus deux points. Si M est l’un de ces points, la droite (IM) coupe l’axe des ordonnées en un point dont l’ordonnée est solution.
· existence des solutions :
soit W le centre du cercle C , r son rayon
on a alors : d(W , (AB))r
b2 – 4ac
0
· limites de la méthode :
a, b et c doivent être choisis dans des limites raisonnables... (...de l’écran)
· intérêt :
- aspect ludique : les élèves peuvent retrouver les racines conjecturées par CABRI à l’aide de leurs calculatrices
- retrouver graphiquement les théorèmes classiques sur le second degré
- que se passe-t-il si a et c sont de signes contraires ? si b = 0 et ac < 0 ?
La
construction CABRI
| Passer en mode
CABRI construction
d’un repère orthonormé mise en place des données
de l’orthogone construction géométrique
des solutions les droites (IM1) et (IM2) coupent l’axe des ordonnées aux points X1 et X2 |
8 : Geometry
2 : New Variable : orthogon F2 4: line F2 2: Point on object F4 3: midpoint F2 3: Intersection Point |
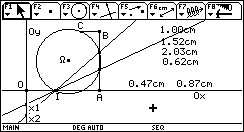
Interprétations
graphiques
Qualitatif |
Quantitatif |
| 1) manipulations
de a laisser a > 0 2) manipulations de
c 3) manipulations
de b |
1) mettre a
à 1 (A doit être le symétrique de O par rapport à I) Retrouver alors  2) créer les segments [IA], [AB],
[BC], [OX1] et [OX2] |
.
; 
; 
