Des triangles équilatéraux dans tous les sens
image de Serge Cecconi (IMAG)
Nous allons dans ce module conjecturer un lieu géométrique avec CABRI, point de départ d’un problème sur les rotations.
| On considère dans le plan euclidien orienté
un triangle équilatéral ABC de sens direct : On
note I le milieu du segment [AB], J celui de [AC], M un
point variable du segment [BC]. 1o) Quel est le lieu géométrique du point O
lorsque M décrit le segment [BC] ? 2o) Démontrer que O est le milieu des segments [IT] et [SJ]. 3o) On suppose dans la suite que M est
distinct du milieu de [BC]. 4o) Soit s
la symétrie de centre O et r
la rotation de centre Q et d’angle
5o) Démontrer que la médiatrice de [PQ] passe par un point fixe indépendant de la position de M. |
![]() Construction
CABRI pour conjecturer le lieu de la question 1
Construction
CABRI pour conjecturer le lieu de la question 1
Lecture de la construction |
Construction Cabri |
|
| Lancer
Cabri
Construire A, sommet du triangle équilatéral Construire le triangle ABC. |
APPS
8 Geometry 3 New Variable : triequi F2 4 Line - F2 2 Point on Object
|
|
| Créer
le point M, objet sur [BC]. Construire alors : - la parallèle à [AB] passant
par M - le milieu O de [PQ] |
F2 2 Point
on Object F2
4 Line |
Figure
finale :
|
Manipulations de la figure : Déplacer M sur le segment [BC]. Observez la figure.
Construire le lieu de O lorsque M décrit [BC]. Vous
n’avez rien vu ? C’est donc que le lieu demandé
est une partie d’un objet déjà apparent. Lequel ? Le
cacher (F7 1 Hide / Show)
et recommencer.
Justifier la conjecture que vous venez d’émettre.
Dénombrez tous les triangles équilatéraux que vous voyez sur cette figure en justifiant à chaque fois. (Cela peut-être long !)
![]() La
figure CABRI II
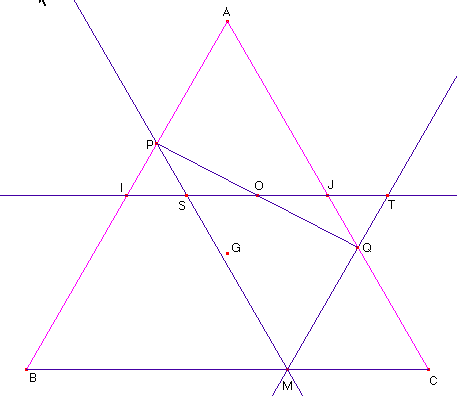
La
figure CABRI II
![]() La
suite du problème
La
suite du problème
Traiter l’exercice de manière classique pour les questions 2, 3 et 4.
Aide à la question 4 :
. décomposeren produit de deux symétries d’axes sécants.
. écrirecomme une rotation puis la décomposer également en produit de deux symétries.
. montrer alors que :
![]() La
figure finale
La
figure finale
A l’aide de CABRI, déplacer le point M et observer la médiatrice de [PQ].
CABRI permet de tracer des lieux de droites. Nous allons donc observer l’ensemble des médiatrices de [PQ] lorsque M décrit [BC] :
F8 9 Format
# of Locus Point : 99
Enveloppe of Lines : OFF
F4 A Locus montrer la médiatrice puis le point M.
On obtient la superbe figure suivante :
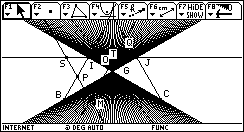
Démontrer alors le résultat que l’on vient de conjecturer.