Introduction
aux probabilités
Lancer de deux
dés cubiques non truqués
Première
partie : introduction, vocabulaire
Le lancer d’un dé est une expérience aléatoire car on n’en connaît pas l’issue au préalable.
Lorsque l’on jette deux dés et que l’on note les sommes des deux nombres lus sur les faces supérieures des dés, quels sont tous les résultats possibles ?
| L’ensemble des résultats
possibles est appelé univers. Appelons W cet ensemble. Lister le contenu de W : W
= |
|
Un événement est un ensemble d’éventualités.
Un événement élémentaire contient une seule éventualité.
Dresser la liste des éventualités de chacun des événements
suivants :
- l’événement A : " Obtenir une somme
paire "
- l’événement B : " Obtenir une somme
multiple de trois "
- l’événement contraire de A (on le note 
) est :
- l’événement D : " Obtenir une somme
paire ou multiple de trois " (
)
- l’événement E : " Obtenir une somme
impaire et multiple de trois " (
)
Représenter sur un diagramme les ensembles A, B, D et E.
Le tableau suivant est une bonne représentation de l’expérience aléatoire. Le compléter.
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
||||||
2 |
||||||
3 |
||||||
4 |
||||||
5 |
||||||
6 |
Quel est la somme la plus probable ? la moins
probable ?
De combien de façons différentes peut-on faire un 7 ?
Quelles sont vos chances d’obtenir un 7 ?
Ce nombre est appelé probabilité de l’événement
" Obtenir une somme égale à 7 ".
A l’aide de ce tableau, donnez
- la probabilité pour que la somme soit égale à 2 ?
- à 11 ?
Expliquez.
Peut-on obtenir une somme égale à 1 ?
On dit que l’événement " Obtenir une somme
égale à 1 " est un événement impossible.
Remplir alors le tableau suivant :
somme xi |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
total |
probabilité pi |
Quelle est la probabilité de l’événement " Obtenir une somme égale à 2 ou 3 ou 4 ou ... 12 " ?
C’est la probabilité d’obtenir l’univers lui-même. On dit que W est un événement certain.
Deuxième partie : approche statistique
Activité préalable à mener par groupe de 2
Chaque groupe de deux élèves effectue 10 lancers de son jeu de
dés et note les sommes obtenues à chaque lancer.
Chaque groupe va comptabiliser au tableau les sommes obtenues
(pour une méthode efficace, pensez aux élections des
délégués de classe) jusqu'à ce que la classe obtienne un
échantillon global de N lancers.
Remplir alors le tableau suivant :
| somme xi | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
total |
| nombre ni d’apparitions de xi | N |
|||||||||||
| fréquence d’apparition ni /N |
1 |
Sur le graphique suivant, représenter la probabilité et la fréquence d’apparition correspondant à chaque somme.
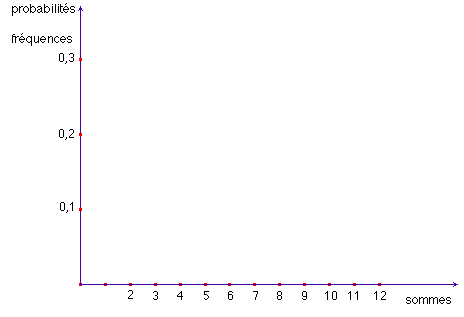
| Que remarquez-vous ? |  |
