| |
Consignes : Le but de ce module est de mettre en équation des problèmes rencontrés en arithmétique, en géométrie, en analyse ou dans la vie de tous les jours. A vous de choisir les inconnues convenablement. On ne demande de résoudre aucun de ces problèmes. |
Problème
1
Pour un triangle ABC, on a :
a = BC =10,
b = CA =12,
c = AB =16.
On trace le cercle inscrit dans
ce triangle, tangent aux côtés du triangle en D, E et F.
a) Calculer les longueurs des segments
AD, DB, BE, EC, CF, FA.
b) Généraliser avec un triangle
de côtés a, b,
c.
Problème
2
 |
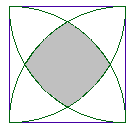Un carré de côté a
a été découpé en traçant quatre quarts de cercles,
centrés en chacun des sommets du carré. Calculer l’aire de la surface grisée. |
Problème
3 : Un problème de Diophante
Une somme S quelconque étant donnée, trouver trois nombres tels que le premier avec la moitié de la somme des autres, le second avec le tiers de la somme des autres et le troisième avec le quart de la somme des autres forment la somme donnée.
Résoudre le problème pour S = 68, puis pour S quelconque.
A quelle condition trouve-t-on des nombres entiers ?
Problème
4
Trouver un nombre à deux chiffres tel que, si on intervertit les chiffres, il augmente de 27 et tel que le double du chiffre des dizaines surpasse de 1 le chiffre des unités.
Problème
5
Emilie ne se souvient plus du nombre de
sandwichs qu’elle a vendus aujourd’hui. Elle a coupé
ce matin 426 tranches de jambon très finement et elle a utilisé
30 baguettes coupées chacune en trois.
Elle confectionne trois types de
sandwich :
- le st-louisien avec 5 tranches de
jambon, de la moutarde et des cornichons, qu’elle vend 12F
pièce;
- le tamponnais avec 3 tranches
de jambon, du fromage et quelques feuilles de salade, vendu 15F
pièce;
- le parisien avec 6 tranches de
jambon et du beurre, et qu’elle vend 13F pièce.
Sa recette en fin de journée est de 1206F pour la vente de ces sandwichs.
En justifiant chaque ligne, écrire un système d’équations permettant de trouver le nombre de st-louisiens, de tamponnais et de parisiens qu’elle a vendus dans sa journée.
Problème
6 : Systèmes pour des courbes
La parabole, le cercle, l’hyperbole, l’ellipse sont des courbes qui sont toutes des coniques.
Dans un repère orthonormal, on
considère les trois points suivants :
A(12; 0), B(–1; –1), C(–2; 5).
Vérifier qu’ils ne sont pas
alignés.
a) Par A, B, C, il passe
un cercle et un seul. Pourquoi ? Préciser son centre et son
rayon.
b) Une seule parabole
d’équation 
passe par A, B et C. Trouvez-la.
c) Une seule hyperbole
d’équation 
passe par A, B et C. Trouvez-la.
d) y a-t-il une seule courbe
d’équation 
passant par A, B et C ?
