Un nombre entier quelconque N peut être considéré comme la valeur numérique d'un
polynôme P(x), le polynôme étant à coefficients entiers positifs, inférieurs à
x, x entier positif ; x est la base de la
numération.
P(x) = amxm + am-1xm-1 + ... + am-pxm-p + ... + a0
Chaque monôme est porteur de deux informations :am-p et
xm-p .
En numération de position, ce nombre N est symboliquement représenté sous la forme
:
am am-1 ......am-p ......a0
Dans une telle écriture, seuls les coefficients subsistent. Il semblerait que la
deuxième information ait été perdue. La seconde information n'est cachée qu'en
apparence puisqu'elle exprime de manière parfaite la position occupée par
am-p dans l'écriture du nombre.
Dans la numération de position, on associe à tout chiffre am-p deux
informations distinctes symbolisées par deux nombres entiers positifs. On peut donc
imaginer une représentation analytique de ce nombre en portant en abscisse, pour chacun
de ses chiffres am-p, le nombre d'unités contenues dans ce chiffre et
en ordonnée, le rang du chiffre considéré (m-p). Il semble que la présentation
analytique du nombre écrit en numération de position ne nous apporte rien de nouveau.
Son intérêt n'apparait que si l'on décide d'égrener les unités composant la valeur
numérique symbolisée par chaque chiffre, sous la forme de cercles égaux, centrés sur
l'axe des X ou sur une parallèle à cet axe. Le nombre considéré apparaît tel qu'il
serait représenté sur un boulier.
Illustrons ceci par un exemple :
Prenons le nombre 1437.
Nous avons :
1437 = P(10) avec P(x) = 1. x3 + 4.
x2 + 3. x + 7
Cette écriture nous fournit les représentations analytiques suivantes, où la valeur
numérique des coefficients est portée en abscisse, et le rang de chaque coefficient en
ordonnée :
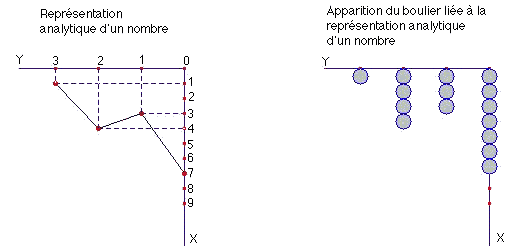
Les créateurs de cet instrument ont donc fait de la géométrie analytique sans le
savoir.
Du boulier, on passe immédiatement à la numération écrite de position à la seule
condition de choisir des symboles pour exprimer tous les nombres inférieurs à la base.
Inversement, on passe, par l'intermédiaire d'une représentation analytique, de la
numération écrite de position au boulier.
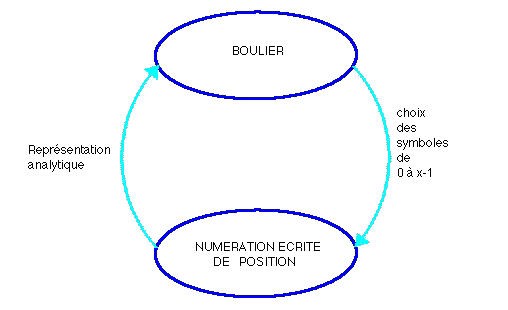
Il existe donc une véritable équivalence entre un nombre présenté sur le
boulier et ce même nombre écrit en numération de position.
Deux calculateurs, qui n'ont pas la même langue mais qui utilisent une numération
écrite de position de même base, représenteront de manière identique un nombre donné
sur leur boulier.
Il s'agit du même nombre puisqu'il est représenté sur le boulier de manière
unique.
La numération figurée la plus parfaite est donc celle du boulier : elle a un
caractère universel pour une base donnée.
Seules, l'unité, la base et les puissances successives de la base seront
représentées sur les tiges du boulier.
L'en-tête a généralement disparu en regard de chacune de ses tiges.
La représentation linéaire d'un nombre écrit en numération de position réduit son
expression analytique à la seule ordonnée.
Il est naturel de commencer par les grandes puissances de la base.
Sur le boulier, en général, le premier nombre inscrit peut l'être de manière
quelconque, l'origine des ordonnées peut ne pas être précisée.
Il est alors indispensable de marquer la place des unités simples par un signe distinct
dans la présentation écrite du nombre et de préciser sur le boulier la position de
l'origine.
Pour obtenir, à partir du polynôme fondamental, la numération écrite de position
de la meilleure qualité, il convenait d'envisager séparément et exclusivement les deux
informations contenues dans chaque monôme de ce polynôme. Ceci est aussi vrai pour le
boulier.
Avec la table à compter, on peut ultérieurement décider de supprimer l'en-tête,
ce qui le présentera sous la forme d'un simple échiquier sur lequel on placera les
cailloux. Que les cailloux soient remplacés par de petits bâtonnets et voici la
numération figurée chinoise. Si l'on va au delà, on peut imaginer de remplacer les
petits cailloux par des billes que l'on enfilera sur des tiges fixées rigidement, à
l'en-tête lui-même indéformable. Et voici le boulier sous sa forme parfaite, instrument
qui a même le mérite d'être portatif.
L'origine commune de la numération écrite de position et du boulier explique
l'identité de leur conception, ce qui a permis aux chinois de présenter le nombre sous
sa forme la plus abstraite.