DocAide Exercices OEF
Plan
Ce document est une introduction à la programmation d'exercices OEF et quelques sources commentés d'exercices. Vous trouverez une présentation des autres documentations utiles dans les conseils de base que vous lirez avant de vous lancer dans la programmation.
Vous pouvez mettre ce document en version imprimable (en haut à droite) pour avoir une vue d'ensemble de son contenu ou faire une recherche sur un mot (à l'aide de la fonction recherche de votre navigateur). Si vous programmez un exercice OEF en même temps, il est conseillé d'ouvrir cette documentation dans un autre signet de votre navigateur.
Les exemples commentés qui émaillent cette présentation sont aussi accessibles par le lien
Une petite flèche bleue vous indique le lien vers un exemple
d'exercice.
![]()
- Structure d'un exercice OEF
- Un premier exemple :

- Programmation
- Questions et réponses
- Exercices à étape
- Matrices
- Dessins
- Insertion d'exemples aléatoires ou d'exercices dans un document wims (voir Rédiger un document).
- Les commandes
- Analyse d'exemples d'exercices
- Le premier dépannage
conseils de base
Le premier exercice dans votre classe
- Dans la page d'accueil de votre classe, cliquez sur Ajouter un exercice. L'interface de Createxo s'ouvre. Vous pouvez l'utiliser pour créer votre exercice ou travailler directement sur le source en passant en mode brut. Les explications de ce document concerne la programmation en mode brut.
- Une fenêtre s'ouvre où vous pouvez écrire le source de votre exercice ou copier des exemples de ce document. Vous pouvez aussi y modifier le source d'un exercice du serveur importé dans votre classe.
Les sauvegardes
Quand vous envoyez le source, vous pouvez tester votre exercice mais il n'est pas enregistré dans votre classe. Ainsi, si vous fermez alors le navigateur, vous ne retrouverez pas votre source la prochaine fois. Pour l'enregistrer la première fois, utilisez le lien mettre cet exercice dans votre classe. Ensuite vous avez le choix entre- remplacer l'ancien (efface la version précédente)
- en faire un nouveau (permet de garder l'ancienne version, mais pensez à changer le titre de la nouvelle version).
Modtool
Vous pouvez aussi créer un exercice dans Modtool si vous avez un compte développeur. Dans Modtool, les exercices OEF sont groupés par modules. Ce sont les modules qui peuvent être publiés (rendus publics).
Utilisation dans une feuille d'exercices
Les exercices de votre classe sont utilisables par les élèves de votre classe si vous faites un lien dans une feuille de travail (insérer).
Documentation
Ce document est une introduction à la programmation des exercices OEF. Il est indispensable de consulter la documentation du serveur. Voici la liste par niveau d'avancement
- FAQ
- Aide dans Createxo.
- Tech doc : on trouve le lien vers cette documentation en bas de la page d'accueil de WIMS. On y trouve en particulier la liste des slib (bibliothèque de macros).
- Si vous utilisez des logiciels à travers wims,
vous pouvez tester vos programmes à l'aide de
Direct exec
.
Comment construire son exercice
Vous n'êtes pas obligé de programmer votre exercice comme l'étudiant le résoudra. Il vaut souvent mieux partir de la réponse pour calculer les données qui apparaîtront dans l'énoncé. Voir Exercice à étape sur les polynômes du second degré .Analyse d'exemples d'exercices
PuissancesExercice à étape sur les polynômes du second degré
Exemple d'utilisation de click avec des images
Exemple élaboré d'exercice utilisant coord
Possibilité d'écrire sur un dessin (réponse à choix)
Un exemple d'exercices où l'élève doit recommencer
Utilisation de matrices dans un exercice de grammaire
Puissances
\title Encadrement de nombres décimaux }
\language{ fr }
\author{ Bernadette Perrin-Riou }
\email{ bpr@math.u-psud.fr}
\computeanswer{ no } \format{ html } \precision{ 10000 } \integer{ n = randint(3..6) } \integer{ p = random(randint(5..7),randint(1..3)) } \real{ a = randint(10^( \n)..10^( \n + 1)-1) } \real{ A = \a/10^(\p) }
\real{ sol1 = \n-(\p) }
\real{ sol2 = \n-(\p) + 1 } \statement{ Donner un encadrement du nombre \( \A)
par des puissances de 10 consécutives.
<center>10<sup><sup>
\embed{ reply 1,4 } </sup></sup>
\leq \A < 10
<sup><sup> \embed{ reply 2,4 } </sup>
</center> } \answer{ exposant }{ \sol1 }{ type = numeric }
\answer{ exposant }{ \sol2 }{ type = numeric } \hint{ Vous pouvez d'abord écrire le nombre avec la notation scientifique. } Le fichier
\title{ Encadrement de nombres décimaux } \language{ fr } \author{ Bernadette Perrin-Riou } \email{ bpr@math.u-psud.fr } \computeanswer{ no } \format{ html } \precision{ 10000 } \integer{ n = randint(3..6) } \integer{ p = random(randint(5..7),randint(1..3)) } \real{ a = randint(10^(\n)..10^(\n + 1)-1) } \real{ A = \a/10^(\p) } \real{ sol1 = \n - (\p) } \real{ sol2 = \n - (\p) + 1 }
\statement{ Donner un encadrement du nombre \(\A) par des puissances de 10 consécutives. <center>10<sup><sup> \embed{ reply 1,4 } </sup></sup> \leq \A < 10<sup><sup> \embed{ reply 2,4 } </sup> </center> } \hint{ Vous pouvez d'abord écrire le nombre avec la notation scientifique. }
\answer{ exposant }{ \sol1 }{ type = numeric } \answer{ exposant }{ \sol2 }{ type = numeric }
Structure d'un exercice OEF
La programmation d'un exercice OEF a une structure linéaire : la position des commandes dans le programme a de l'importance. On peut distinguer trois zones importantes du programme que nous allons détailler et dont l'exécution correspond à des actions pratiques précises.
Nous les appellerons Avant, Pendant, Après :
Un exemple simple Voici le fichier d'un exercice qui demande de calculer le carré d'un entier choisi aléatoirement et met un avertissement si la réponse donnée est négative :
Avant :\title{ Le carré d'un entier } \computeanswer{ no } \integer{ n = randint(-50..50) } \integer{ N = \n^2 }Pendant :\statement{ Calculer le carré de \n. }Après :\answer{ Carré de \n }{ \N }{ type=numeric } \feedback{ \reply1 < 0 }{ Le carré d'un entier est toujours positif. }
Dans cette partie du programme on trouve en particulier :
-
Instructions générales concernant l'auteur et l'exercice
\title{ }
\language{ }
\author{ }
\email{ }
\format{ }
\precision{ }
\range{ }
\computeanswer{ } - Définitions de variables :
\text{ a = }
\integer{ a = }
\rational{ a = }
\real{ a = }
\complex{ a = }
\matrix{ a = }
\function{ a = } - tous les calculs nécessaires en utilisant les variables déjà définies pour écrire l'énoncé
- les calculs pour la réponse ne demandant pas de connaître la réponse de l'utilisateur
On utilise une variable déjà définie en la faisant précéder par
un
\ :
\integer{ a = 3 + 4}
\integer{ b = (\a)^2}
\real{ c = sqrt(\a)}
\statement{ Enoncé de l'exercice }
\help{ Aide en popup }
\hint{ Indication}
Dans cette partie, on peut utiliser
- toutes les variables définies dans la partie Avant.
- le mode mathématique ou les commandes html pour la mise en forme, voir le document DocAide Documents
Les cases de réponses peuvent être "immergées" dans le statement ( voir Immersion des cases de réponses )
Attention :
- ne pas utiliser \text{ a = } .... dans les champs \statement, \feedback, hint.
- un seul \statement{ } . Si vous voulez faire plusieurs étapes, c'est la commande \steps qu'il faut utiliser.
Pour cela, il faut déclarer les questions et leurs réponses ainsi que la manière dont elles doivent être analysées. C'est le rôle du type :
\answer { Commentaire }{ \reponse }{ type = mot_reserve}
\choice{ Commentaire }{ \bonchoix }{ \tousleschoix }
Le type est donc quelque chose de très important, il détermine à la fois quel style de réponses est demandé (click, clickfill ou numeric) et comment elles vont être testées (voir les différences entre formal ou algexp ou function).
On peut alors faire une analyse plus précise des réponses avec la commande \condition, utiliser les réponses fournies par l'utilisateur, renvoyer des commentaires (\feedback ou \solution). Si besoin, on peut définir des variables et faire des calculs comme dans la première partie.
- créer un exercice demandant de calculer la somme
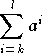 en choisissant aléatoirement les paramètres k, l et a.
en choisissant aléatoirement les paramètres k, l et a.
Faire un feedback si le calcul semble avoir été fait avec une erreur standard (à vous de voir). - modifier l'exercice précédent pour en faire un exercice à deux étapes, en demandant en deuxième question si la suite
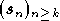 définie par :
définie par : 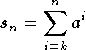 a une limite lorsque n tend vers
a une limite lorsque n tend vers 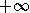 .
.
Variables
La plupart des commandes de variables se trouve dans l'aide de Createxo . Mais il vaut mieux l'avoir un peu "feuilleté" pour y trouver ce que l'on a besoin. Dans la rubrique Paramètres aléatoires dans un exercice interactif, il y a la plupart des fonctions ou procédures accessibles.-
Introduire les premières données
On peut mettre des données textes, numériques, matricielles. On peut aussi manier des expressions "Tex" que l'on met alors dans \( ).
\rational{ x = 1/5 + 3/4 } \real{ y = 1/5 + 3/4 } \text{ z = 1/5 + 3/4 } \integer{ t = 2.6754 }Ici, x est un rationnel, y est donné comme un réel avec décimales, quant à z, c'est exactement 1/5 + 3/4.Pour le dernier, t est l'entier le plus proche de 2.6754.
\text{ liste = 1,2, x, 3/4 } \text{ liste = \(\forall), \(\exists), \(\in) } \matrix{ A = 1,2,3 2,3,4 4,5,6 } \matrix{ A = la fonction est positive, oui la fonction est négative, non }Une matrice peut ne pas avoir toujours le même nombre de colonnes, comporter du texte de toutes sortes. Une matrice peut servir à stocker, par ligne, les données, l'énoncé et la bonne réponse d'une question aléatoire. -
Récupérer des données dans une liste ou une matrice
\text{liste = 1,2, x, 3/4} \matrix{A = la fonction est positive, oui la fonction est négative, non} \text{s = item(3,\liste)} ou \text{s = \liste[3]} \text{s = item(1,row(2,\A))} ou \text{s = \A[2;1]}D'autres mots : column, row, item, randitem -
L'aléatoire
-
autour
du mot random
\real{ x = random(-5..5) } \integer{ y = random(-5..5) } \integer{ y = randint(-5..5) } \function{ f=random(x^2+1,sin(x),log(x)) } \rational{ z = randint(-5..5)/randint(1..7) } \text{ t = random(1,2,3,a,b,c) } \text{ t = randitem(1,2,3,a,b,c) } \text{ l = randomrow(1,2,3 2,3,4 4,5,6) }Toutes ces commandes permettant d'obtenir un résultat choisi au hasard parmi un ensemble d'objets. - Pour les plus avancés : on peut aussi utiliser des scripts
pour obtenir des objets aléatoires plus évolués :
par exemple,
\text{ A = slib(matrix/non0 5,10,100) }donne une matrice de taille 5,10 avec des coefficients non nuls bornés par 100\text{ A = slib(stat/binomial 100, 5,0.1) }produit une liste de 100 nombres vérifiant une loi binômiale de paramètres 5 et p = 0.1 .Un autre exemple :\text{ mot = randitem(aluminium, fer, bauxite) } \text{ A = slib(lang/frapostrophe de \mot) }le résultat est selon le cas, d'aluminium, de fer ou de bauxitePour trouver la liste des commandes, SLIB
-
autour
-
Faire des calculs
Un certain nombre de fonctions mathématiques sont toutes intégrées. Une liste se trouve dans l'aide de Createxo.
On peut avoir des fonctions plus avancées à l'aide de logiciels de calculs que WIMS appelle. Les plus importants sont
- PARI/GP
- Maxima
On trouvera des exemples dans les exercices commentés.
Juste un avertissement :
\text{ g = -x + y } \text{ f = x*\g } \text{ h = - \g } \statement{ h = \h; f = \f }Attention à bien mettre des parenthèses où il faut. Ici, \g est remplacé par -x + y ce qui ne fait peut-être ce que vous attendiez.
Boucles et branchements
On peut utiliser des boucles et des branchements à la fois pour la définition des variables et dans la partie statement.
\if{ \a = 1 }{\text{ b = 2}}{\text{ b = 3 }}
\text{ b = \a = 1 ? 2 : 3 }
\for{ i = 1 to 10 }{ \text{ b = \b,\i } }
\integer{ k = 1 }
\text{ b = \k }
\while{ \k < 10 }{
\integer{ k = \k+1 }
\text{ b = \b,\k }
}
Voici un exemple dans la rédaction d'un énoncé :
\text{ a = randint(1..2) }
\statement{ On tire \a \if{ \a = 1 }{ boule }{ boules}. }
Exemples de slib
Il existe une bibliothèque de macros qui sont créées au fur et à mesure des besoins des utilisateurs. Voici quelques thèmes concernés par ces macro slib : chimie, graphe, langue, matrice, statistique, dessin.
Pour accéder à la liste des macros existant sur le serveur, cliquer sur WIMS technical documentation Si vous cliquez sur une des commandes, vous obtenez un tableau dans lequel sont indiqués le nom, la signification des paramètres et de temps en temps un exemple de même que la syntaxe à utiliser (Call from OEF / DOC) :
Pour l'utiliser dans un exercice, la syntaxe est la suivante :
\text{ resultat = slib(nom parametre) }
Voici quelques exemples, mais le mieux est que vous alliez voir.
pour dessiner
Exercice utilisant coord :
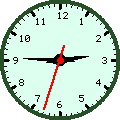
draw/clock
\text{ horloge =slib( draw/clock 02:45:33, 120) }
\statement{ \draw{ \horloge}}
lang/frapostrophe
\text{ cheval = slib( lang/frapostrophe de le cheval) }
\text{ ane = slib( lang/frapostrophe de le âne) }
Résultat : du cheval, de l'âne
Cela est commode si vous voulez faire des énoncés en français par exemple l'atome de chlore, d'oxygène où l'élément chimique est pris au hasard.
\text{ atome = randitem(chlore,oxygène,carbone,hydrogène) } \text{ datome = slib( lang/frapostrophe de ) }
text/comblin
\text{ a = slib(text/comblin [1,2,3] , [\vec{e_1}, \vec{e_3}, \vec{e_2}]) } \statement{ \(\a) }
stat
On trouvera- des macros permettant de faire une analyse statistique de données, par exemple
stat/mean, stat/variance, stat/effectif, stat/histo ...
- des macros pour déterminer la valeur de la
densité, de la fonction de répartition ou des quantiles de lois
classiques. Les noms de ces macros sont tous fabriqués de la même
manière :
stat/???pdf stat/???cdf stat/???inv
où ??? est à remplacer par le nom d'une loi classique.
Exemple :\text{ res = slib(stat/binomialcdf 3,10,0.5) }
- des macros permettant de générer des réalisations de variables aléatoires. Exemples :
- stat/empiric pour générer des réalisations d'une variable aléatoire discrète dont on spécifie les coefficients :
\text{ jeu = slib(stat/empiric 5,[2/3,1/3],[pile,face]) }
-
\text{ A = slib(stat/normal 10,0,2) }
-
stat/posdiscretelaw pour générer les coefficients d'une
loi de probabilité sur un ensemble fini dont les coefficients sont
strictement positifs
\text{ proba = slib(stat/posdiscretelaw 7,10,Q) }
Commandes wims
Certaines des commandes que l'on trouve dans la documentation technique WIMS technical documentation sont utilisables à travers la commande wims et donnent de grandes facilités de manipulation de texte. Par exemple :
\text{ S = wims(values x^2 for x = 1 to 10) }
\text{ S2 = wims(values exp(x) for x in \S) }
\text{ S3 = wims(nospace a b ) }
\statement{ S = \S;
S2 = \S2 ; S3 = \S3 }
\text{ A = 3,6,8,9,2 }
\text{ S = wims(replace internal item number 4 by z in \A) }
\text{ T = wims(replace internal 3 by oui,non in \A) }
\statement{ A = \A; S = \S; T = \T }
\text{ L = 1,3,7,8,9,10 }
\text{ L= wims(replace item number 3 by non in \L) }
\text{ L = 1,3,7,8,9,10 }
\text{ L= wims(replace item number 3 by in \L) }
\text{ L= wims(nonempty items \L) }
\text{ L = 1,3,7,8,9,10 }
\text{ L= wims(replace item number 3 by \L[3],oui in \L) }
\text{ L = wims(values x^2 for x = 1 to 20) }
\text{ L = wims(makelist r x for x = 1 to 20) }
Utilisation de logiciels
Nous ne parlons ici que de l'utilisation d'un logiciel dans un exercice OEF, bien qu'il en soit de même (souvent plus simple) dans un module WIMS. Si vous ne disposez pas de ces logiciels, vous pouvez les utiliser et faire vos tests à travers Direct exec .
Comment appeler le logiciel
De manière générale, on appelle un logiciel en utilisant la commande exec à travers wims\text{ a = wims(exec povray ...) }
\text{ a = wims(exec octave ...) }
Ce qui remplace ... sont des commandes du logiciel.
Il y a deux cas particuliers : pari et maxima.
\text{ a = pari( ...) }
\text{ a = maxima(....) }
Maxima :
Documentation Maxima
\text{ f = sin(x)/x^3 }
\text{ f = maxima(diff(\f,x,2)) }
Octave :
\real{ a = randint(1..10)/10 }
\text{ fonct = 2*t*x }
\text{ reponse = wims(exec octave
function
xdot=f(x,t)
xdot=\fonct;
endfunction;
lsode("f",1,(t=[0,\a])) }
GP/PARI :
Documentation GP/Pari
\integer{ n = randint (20..23) }
\text{ N = pari(factor(\n!+1)) }
factor(20!+1) = 20639383,1;117876683047,1
![]() Base de l'image d'une application linéaire.
Base de l'image d'une application linéaire.
Pour plus de détails : Utilisation de Pari .
Réutiliser des commandes
Dans un module OEF, le logiciel reste ouvert entre deux exécutions et l'on peut donc garder des routines ou des variables "ouvertes". Un exemple :\text{ essai_pari = pari( (f(x) = local(t) ; t=x^2 ; t)) }
\text{ data_pari = pari(a = 2 ; M = 3)
\integer{ n = randint(2..8) }
\text{ f1 = pari(f(\n)) }
\text{ f2 = pari(f(M)) }
\text{ a = pari(a) }
\text{ b = \a^2 }
\text{ c = pari(a^2) }
Ici, \n appelle une variable définie par wims,
M un entier défini dans Pari/GP et appelé par Pari/GP,
a est à la fois une variable de WIMS et de Pari/GP
et donc on l'appelle par \a dans WIMS et par
a dans GP/Pari.
Résultats : essai_pari= ; f1 = 36 ; f2 = 9 ; a = 2 ; b = 2^2 ; c = 4 ; M = M ; f = -sin(x)/x^3+12*sin(x)/x^5-6*cos(x)/x^4 .
Utilisation de programmes internes aux logiciels de calcul
Il est possible d'entrer des programmes dans le langage des logiciels appelés et de les réutiliser ensuite.Voir des exemples dans Utilisation de Pari
Quelques paramètres par défaut
WIMS :precision=10000, print_precision=8PARI/GP :
pari_precision=18
Maxima :
maxima_precision=print_precision
expon:0; expop:0; factlim:6; prederror: false;
maxnegex:20; maxposex:20; ratfac:true; keepfloat:true;
Quelques difficultés pouvant être rencontrées
Chaque logiciel a sa manière de prendre les données et de les ressortir. WIMS essaie dans la mesure du possible de passer de l'un à l'autre. Il y a quand même quelques petits problèmes.Celui qu'on rencontre en premier est le problème des matrices : Une matrice dans GP/Pari ou Octave est de la forme [1,2,3;1,4,5]. GP/Pari renvoie une matrice sous la même forme, mais pas Octave. Et de toute façon, WIMS enlève les crochets de la matrice :
\text{ A = [1,2,3;4,5,6] }
\text{ Aoct = wims(exec octave [1,2,3;4,5,6]) }
\matrix{ Aoct2 = wims(exec octave [1,2,3;4,5,6]) }
\text{ Apari = pari( [1,2,3;4,5,6]) }
Aoct = Aoct2 = Apari = 1,2,3;4,5,6
Octave passe des lignes et Aoct est formé de lignes et les éléments d'une ligne sont séparés par des espaces. On peut utiliser un slib pour la remettre sous forme "normalisée" (sans crochets quand même).
\text{ Boct = slib(text/octavematrix \Aoct) }
Boct =
Autre exemple :
\text{ matrice = wims(exec octave
[5^2 *4 + 5,2,3;5,6,7]) }
\text{ matrice = slib(text/octavematrix ) }
matrice =
Présentation des questions
Il ne suffit pas de poser les questions dans l'énoncé. Pour chaque case de réponses que l'on désire ouvrir, on doit écrire une ligne du type
\answer{ }{ }{ type = xxx}
ou
\choice{ }{ }{ }
Pour \answer : la manière dont la réponse est analysée dépend du troisième argument qui est de la forme type = xxx. Voir Types de réponses pour la liste des types possibles.
Le premier argument est un texte libre, le troisième indique le type de réponses qui est demandé, le second est selon le type la réponse ou une matrice liée à la réponse. Deux autres arguments sont optionnels : { option=} et { weight=}
Il doit donc y avoir autant de lignes avec \answer ou \choice que de questions que l'on désire poser.
Conseils plus avancés
- On peut avoir envie d'immerger des cases de réponses dans l'énoncé.
On utilise la commande \embed
La commande \embed permet d'inclure la zone de réponse dans l'énoncé (documentation complète dans l'aide de Createxo)
\embed{ reply 2 } \embed{ choice 1 }Les mots reply 2, reply2 et r2 sont les seuls admis et sont équivalents (2 peut être remplacé par un entier et renvoie au numéro de la question déterminée par sa position dans les listes des \answer pour les reply ou dans les listes des \choice pour les "choices").
Voici quelques exemples d'utilisations de \embed:
- dans un exercice à étapes (partie détaillée plus tard )
- dans un tableau tableau
-
Il est conseillé avec les types
menu, radio, etc

\embed{ r1 } peut avoir un deuxième argument permettant de fixer la taille de la case de réponses. On renvoie aux différents types où cela est utile (aide OEF et exemples)
- La notation est imposée par l'analyse de la réponse. Cependant vous pouvez influer sur le poids des questions en utilisant l'option weight afin de donner des poids différents aux questions.
- Vous pouvez avoir besoin d'avoir un Nombre variable de réponses
- On peut utiliser des dessins pour poser une question ou obtenir une réponse : Utilisation des dessins dans les questions
Types de réponses
Il y a plusieurs types de réponses possibles. Il est important de maîtriser les nuances (et de tester ...) car la qualité de l'exercice en dépend. En effet, si la réponse fournie n'est pas interprétée comme on veut, la note va s'en ressentir.L'aide en ligne est très complète sur ce sujet. Il est donc conseillé d'aller la consulter : Comment un utilisateur peut répondre à un exercice. Aide . De plus de nouveaux types de réponses apparaissent.
Grâce à WIMS, vous pouvez traiter ( pour revenir à cette page, utiliser la flêche Hist).
-
Du texte
atext case nocase wlist
- Du numérique
- Des fonctions
-
Des ensembles
On conjugue ces types à partir de set
Comparer les réponses possibles dans l'exemple suivantset tel quel aset approximatif expressions numériques fset formal expressions formelles chset liste de caractères alphanumériques \function{ f = sin(x + 2 - 3) } \function{ g = sin(x - 1) } \function{ h = sin(x - 4 + 2) } \function{ t = simplify( \f) } \statement{ \f,\g,\h,\t } \answer{ }{ \f,\g,\h }{ type = fset } \answer{ }{ \f,\g,\h }{ type = aset } \answer{ }{ \t,\g,\h }{ type = fset }Si l'on répond sin(x - 1), sin(x - 1), sin(x - 2), les deux premières réponses sont fausses mais la troisième est juste. Un principe de sagesse : toujours faire simplifier les expressions ... -
D'autres types mathématiques
matrix vector equation units sigunits
- Types à choix
- Des types graphiques
numeric
\computeanswer{ yes }
\real{ a = sqrt(2) }
\statement{ rentrer a = \(sqrt(2)) }
\answer{ }{ \a }{ type = numeric }
Pour une précision relative 1/M, la réponse numérique r est acceptée pour la solution demandée s si et seulement si:
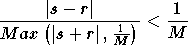
- si
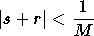 , il est vérifié que
, il est vérifié que
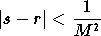 ;
;
-
si
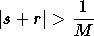 , il est vérifié que
, il est vérifié que
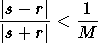 .
.
Avec \computeanswer{ yes } ,
des expressions comme sqrt(2) sont acceptées ainsi que 1 + 2.
Types à choix
Ces types permettent de disposer de manière variée
les questions à choix. Ils sont utilisés en liaison
avec \embed.
L'utilisation de la commande shuffle
permet que les choix ne soient pas toujours donnés
dans le même ordre :
![]()
Essayez-en un et changez le type pour un de ceux de la liste.
menu
\text{ a=oui, non, pourquoi pas }
\text{ rep=1 }
\statement{ Répondre oui :
<center>\embed{ reply1 } </center> }
\answer{ }{ \rep;\a }{ type=menu }
click
radio
checkbox
Premier exemple :
\text{ a = oui, non, pourquoi pas }
\text{ rep = 1,2 }
\statement{ Répondre oui ou pourquoi pas :
<center>\embed{ reply1 } </center> }
\answer{ }{ \rep;\a }{ type=checkbox }
Deuxième exemple :
\text{ a = oui, non, pourquoi pas }
\text{ rep = 1 }
\statement{ Répondre oui :
<ul>
<li>\embed{ reply1,1 } </li>
<li>\embed{ reply1,2 } </li>
<li>\embedreply1,3 } </li>
</ul> }
\answer{ }{ \rep;\a }{ type=checkbox }
??
dragfill
clickfill
correspond
coord
compose (comparer à dragfill et clickfill)
Réutilisation des réponses
Vous pouvez réanalyser les réponses envoyées par l'étudiant,
- parce que les analyses automatiques ne vous plaisent pas
- pour faire un feedback
- (plus avancé) pour décider de la question suivante
Remplacement des réponses analysées automatiquement
Au lieu de mettre la bonne réponse dans le deuxième champ de answer, mettez un nom de variable non encore utilisée\answer{ Réponse }{ \nouvelle_var }{ type=numeric } \condition{ commentaire du test }{ \nouvelle_var = 1 or \nouvelle_var = 2 }
Pour une untilisation plus avancée (dans le cas d'un nombre variable de conditions), voir Condition .
Options
Si vous ne désirez pas que ces conditions apparaissent dans le texte de l'analyse de la réponse, par exemple parce que vous préférez rédiger vous même un commentaire dans un feedback, utilisez l'option option=hide. Vous pouvez aussi mettre des poids sur les conditions weight=\condition{ condition à cacher }{ \reply1 > 2 }{ option=hide }{ weight=1 }
\condition{ condition à cacher }{ \reply1 > 3 }{ option=hide }{ weight=5 }
Faire un feedback
\feedback{ \reply1 = 3 }{ commentaires }
\solution{ texte expliquant la solution }
Les mots \reply1 ... sont des mots réservés. Dans le cas de types de réponses compliqués, faites les afficher dans un feedback (ils ne contiennent pas toujours ce qu'on attend).
\feedback{ 1=1 }{ }
Tests préliminaires
Vous pouvez faire des calculs utilisant les réponses de l'étudiant comme dans la première partie ("Avant").Un exemple d'analyse de réponses sur un texte Test sur un texte
Précision
Dans le cas d'un exercice où une réponse numérique est demandée, les deux commandes \precision{ } et \computeanswer{ } sont importantes
- \precision{ 1000 } indique la précision (relative)
demandée
 Travail
Travail
- \computeanswer{ no} indique que le calcul doit
être effectué par l'élève.
 Exemple à écrire
Exemple à écrire
Exercices à étape
Un exercice à étapes est un exercice qui ne pose pas toutes les questions à la fois. On pose des questions, si la réponse est juste, on en pose d'autres ...
Etapes dont on peut précalculer toutes les questions
On utilise une commande \steps qui crée automatiquement une variable \step. A chaque fois que l'utilisateur clique sur Répondre, la variable \step est incrémentée de 1. On peut donc l'utiliser pour décider quel texte doit être vu à un moment donné.
![]() Exercice à étape sur les polynômes du second degré
Exercice à étape sur les polynômes du second degré
Nombre variables de questions
Vous avez besoin d'un nombre variables de questions selon les données aléatoires. c'est la commande \step qui vous permettra de résoudre ce problème : on introduit à la fin du source un nombre trop important de \answer{ }{ }{ } et on indique dans \steps{ } les réponses effectivement demandées en fonction des variables aléatoires.\text{ n = randint (3..5) }
\text{ STEP = wims(makelist r x for x = 1 to \n) }
\steps{ \STEP }
Etapes qu'on ne peut pas précalculer
Dans certains cas, on désire proposer une suite à l'exercice selon ce qu'aura répondu l'élève et qu'il n'est pas possible de prévoir totalement. Dans ce cas, on ne peut pas définir au départ la liste des r1,..., r10. La commande \steps qui permet de décrire la liste des questions-réponses pour chaque étape est remplacée par la commande \nextstep
- On initialise la liste des reponses demandées à la première
étape dans une variable var (appelée dans les exemples
nstep) :
\text{ var = r1, r2 } \nextstep{ \var } - on redéfinit la variable var après le
statement pour obtenir la liste des réponses à l'étape suivante
(selon les conditions imposées par l'exercice). Le numéro de l'étape
est alors donnée par la variable step comme dans le
cas d'un exercice à étapes classique et peut être utilisée dans les conditions de définition de var.
Matrices
Une matrice dans wims est un tableau pouvant avoir un nombre variable de colonnes selon les lignes.
On le déclare par la commande \matrix{ A = } en allant à la ligne pour chaque nouvelle ligne. Le séparateur sur une ligne est la virgule.
\matrix{ ma_matrice=voici,voilà
un chien, un chat, une porte }
-
Pour récupérer dans l'exemple précédent les mots
une porte, on tape
\text{ a = \ma_matrice[2;3] } -
Pour récupérer la première ligne :
\text{ a = \ma_matrice[1;] } -
Pour récupérer la deuxième colonne :
\text{ a = \ma_matrice[;2] }
Remarque : Il faut savoir qu'en interne, la matrice \ma_matrice est
voici,voilà;un chien, un chat, une porteIl faut donc faire attention aux virgules ou points-virgules qui seraient dans le texte et les remplacer préventivement par le code html ( , , et ; ;).
Utilisation des matrices pour réaliser des exercices
Une matrice n'a pas seulement une utilité en mathématiques, mais permet de stocker des données, par exemple celle d'un QCM.
Utilisation en mathématiques
Mais une matrice garde une utilité en mathématiques à condition de l'utiliser ensuite dans le logiciel pari : Utilisation de Pari
Transformation en html
Vous trouverez ici le code pour mettre une matrice dans un tableau en html : Transformer une matrice en matrice html
Utilisation de slib
- text/matrixtex
\matrix{ A = \vec{e_1}, \vec{e_2}, \vec{e_3} 2,3,4 } \text{ a = slib(text/matrixtex [\A] , lbrace,rvert) } \statement{ \(\a) }Ecrit une matrice en tex, en option lbrace, lvert, ... selon le type de matrice que l'on veut. - matrix/givenrank
\text{ a = slib(matrix/givenrank 4,5,2, 50) } \statement{ \(\a) }Retourne une matrice de taille 4 fois 5 qui est de rang 2 et dont les coefficients sont bornés par 50 - matrix/random
\text{ a = slib(matrix/random 4,5,50) } \statement{ \(\a) }Retourne une matrice de taille 4 fois 5 dont les coefficients sont bornés par 50Dessins
Documentation
La documentation complète des commandes utilisables dans un dessin se trouve dans l'aide de Createxo. Nous attirons votre attention sur le fait que WIMS propose deux commandes draw légèrement différentes pour obtenir des dessins.-
La commande \draw
\draw{ 200, 200 }{doit être utilisée à l'intérieur de \statement{} , \feedback{ }{ } Elle produit un dessin de taille 200 pixels sur 200 pixels défini par les lignes écrites.
ligne1
ligne2
ligne3 } -
La fonction draw()
La fonction draw appelée à travers une commande de définition de variables :
\text{ url_dessin = draw(200,200 ligne1 ligne2 ligne3) }produit l'adresse html du dessin. Comme toutes les définitions de variables, cette définition de url_dessin doit se trouver en dehors de \statement. Pour faire apparaître le dessin, on écrit\statement{ <img src="\url_dessin"> }Les options html de src sont alors utilisables.\text{ A = draw(200,200 xrange -1,1 yrange -1,1 hline 0,0,black fill 0,1,red) } <center> <img src = "\A"> </center>
Exemples
- des exemples de Dessin
- des exemples dans des exercices :
 Nœud
Nœud
 Equation d'une droite affine.
Equation d'une droite affine.
- On peut utiliser des dessins pour poser une question ou obtenir une réponse. Voir l' Utilisation des dessins dans les questions
Avancé
Dans certains exercices (utilisation du type coord sur une image fabriquée, insertion d'une première image dans une seconde), on a besoin du nom de l'image. On le récupère de la manière suivante : la ligne\text{ url_dessin = draw(200,200 ligne1 ligne2 ligne3) } \text{ nom_image = slib(oef/insfilename) }La dernière ligne doit être juste après la définition du dessin (et en tout cas avant le dessin suivant).
Les commandes
Commandes (les * désignent des commandes dont je ne suis pas sûre qu'elles existent, en tout cas non testées par moi).
\author : \author{ xxx } \title : \title{ xxx } \answer : \answer{ blablabla }{ }{ type = xxx }{ weight = yyy } \choice : \choice{ xxx }{ test }{ } \computeanswer : \computeanswer{ yes } \condition : \condition{ blablabla }{ test }{ option=hide } (dernier champ optionnel) \conditions : \conditions{ 1,2,3 } \email : \email{ xxx } \feedback : \feedback{ test }{ blablabla } \format : \format{ html } \help : \help{ xxx } \hint : \hint{ xxx } \next : \next{ xxx } \nextstep : \nextstep{ xxx } \reply : \reply{ xxx }{ }{ }{ } = \answer{ }{ }{ } \solution : \solution{ xxx } \statement : \statement{ xxx } \steps :\steps{ reply1, reply2 reply3,reply4 }ou\steps{ r1, r2 r3, r4 }(pas d'autres lettres que r) \complex : \complex{ xxx = yyy } \function : \function{ f = x^2 } \language : \language{ fr } \precision : \precision{ 1000 } \range : \range{ -5,5 }\for : \for{ i=1to 5 }{ } \if : \if{ test }{ }{ } Il n'y a pas d'évaluation préliminaire des deux membres de la condition ? : \text{ a = condition ? xx : yy } ici condition est évaluée. Sans troisième argument , la variable a n'est pas modifiée si condition est faux
\while : \while{ test }{ }
\integer : \integer{ a = yyy } \matrix : \matrix{ a = yyy } \rational : \rational{ r = 3/2 } \real : \real{ r = 3/2 } \text : \text{ xxx }Autres : permettent la définition des variables*variable : \variable{ xxx } *mdef : \mdef{ { xxx } *parameter : \parameter{ xxx } *plot : \plot{ xxx }
column : \text{ a = column(1,xxx) } deriv : \text{ a = deriv(xxx,x) } derivative : \text{ a = derivative(xxx,x) } det : \text{ a = det(xxx) } diff : \text{ a = diff(xxx,x) } draw : \text{ a = draw(xxx) } evaluate : \text{ a = evaluate(x^2,x = 2) } evalue : \text{ a = evalue(x^2, x = 2) } htmlmath : \text{ a = htmlmath(xxx) } int : \text{ a = int(x^2,x= 0 .. 2) } integral : \text{ a = integral(xxx) } integrate : \text{ a = integrate(xxx,x=1 .. 2) } item : \text{ a = item(1,xxx) } items : \text{ a = items(xxx) } mathexp_cut : \text{ a = mathexp_cut(xxx) } maxima : \text{ a = maxima(xxx) } pari : \text{ a = pari(xxx) } pickone : \text{ a = pickone(xxx) } position : \text{ a = position(xxx) } positionof : \text{ a = positionof(xxx) } randint : \text{ a = randint(xxx) } randitem : \text{ a = randitem(xxx) } random : \text{ a = random(xxx) } randomitem : \text{ a = randomitem(xxx) } randomrow : \text{ a = randomrow(xxx) } randtow : \text{ a = randtow(xxx) } row : \text{ a = row(2,xxx) } rows : \text{ a = rows(xxx) } shuffle : \text{ a = shuffle(xxx) } simplify : \text{ a = simplify(xxx) } slib : \text{ a = slib(xxx)} solve : \text{ a = solve(xxx) } texmath : \text{ a = texmath(xxx) } wims : \text{ a = wims(xxx) } permet d'utiliser du code wims. yacas : \text{ a = yacas(xxx) }Noms ayant une signification imposée :
imagedir : \imagedir confparm1 : \confparm1 confparm2 : \confparm2 confparm3 : \confparm3 confparm4 : \confparm4 step : \step r1 : r1 pour reply1
Gestion des tableaux :
\matrix{ A = x,y,z u,v,t } \statement{ \A[1;3] }solve
Le premier dépannage
Votre programme ne marche pas ?
- Vérifiez que vous n'avez pas oublié un \ avant une variable déjà définie et que vous désirez réutiliser.
- Si vous avez mis des conditions, n'oubliez pas que le signe = ne teste que des valeurs numériques. Dans le cas de texte, utiliser issametext ou autre (voir la liste dans l'aide en ligne).
- On vous dit qu'il y a une faute de syntaxe dans compare.
Peut-être avez-vous un point d'interrogation dans une définition de
variables et cela est incompatible avec la structure de test
\text{ a = condition? resultat1:resultat2 }Vous devez écrire le code html correspondant au point d'interrogation. Codes utiles
-
La commande \draw
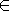
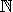 * pour tout
i et
p1+...+p7=1.
* pour tout
i et
p1+...+p7=1.